Gamma Function
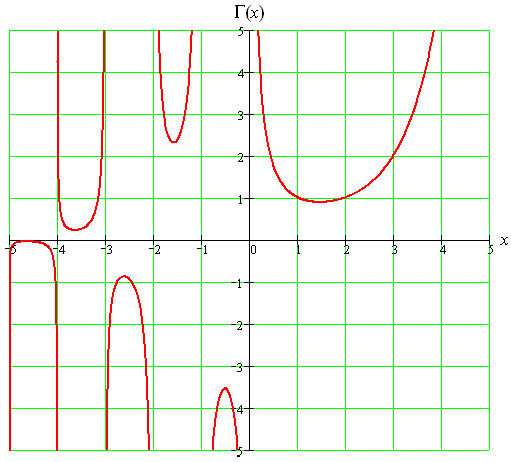In mathematics, the gamma function is an extension of the factorial function, with its argument shifted down by 1, to real and complex numbers.
The gamma function is a very common special function, which finds application in such diverse areas as quantum physics, astrophysics, and fluid dynamics.
The gamma distribution, which is formulated in terms of the gamma function, is used in statistics to model a wide range of processes.
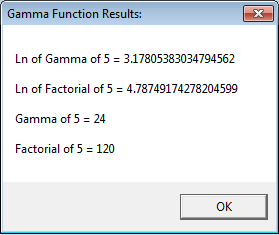
The source code presents an accurate estimation of the gamma function and factorials both on the absolute and the logarithmic scale.
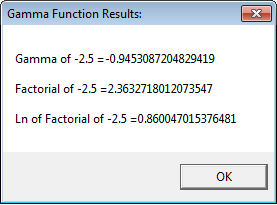
The arguments can be all real numbers except negative integers. The source code uses Euler’s reflection formula to estimate gamma for negative numbers.
[code language="vb"]
#COMPILE EXE
#DIM ALL
FUNCTION GammLn(BYVAL x AS EXT) AS EXT
' Returns Ln(Gamma()) or 0 on error
' Based on Numerical Recipes gamma.h
' Lanczos, C. 1964, "A Precision Approximation
' of the Gamma Function," SIAM Journal on Numerical
' Analysis, ser. B, vol. 1, pp. 86-96.
LOCAL j AS LONG, tmp, y, ser AS EXT
DIM cof(0 TO 13) AS LOCAL EXT
cof(0) = 57.1562356658629235
cof(1) = -59.5979603554754912
cof(2) = 14.1360979747417471
cof(3) = -0.491913816097620199
cof(4) = 0.339946499848118887e-4
cof(5) = 0.465236289270485756e-4
cof(6) = -0.983744753048795646e-4
cof(7) = 0.158088703224912494e-3
cof(8) = -0.210264441724104883e-3
cof(9) = 0.217439618115212643e-3
cof(10) = -0.164318106536763890e-3
cof(11) = 0.844182239838527433e-4
cof(12) = -0.261908384015814087e-4
cof(13) = 0.368991826595316234e-5
IF x <= 0.0 THEN FUNCTION = 0.0 : EXIT FUNCTION ' Bad argument
y = x
tmp = x + 5.2421875
tmp = (x + 0.5) * LOG(tmp) - tmp
ser = 0.999999999999997092
FOR j = 0 TO 13
y = y + 1
ser = ser + cof(j)/y
NEXT j
FUNCTION = tmp + LOG(2.5066282746310005 * ser / x)
END FUNCTION
'
FUNCTION PBMAIN () AS LONG
LOCAL s1, s2, s3, s4, X, X1, PI AS EXT, t, t2 AS STRING
PI = 4.0 * ATN(1.0)
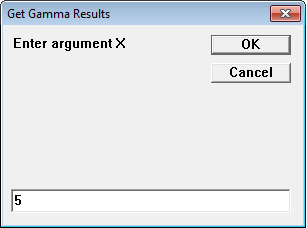
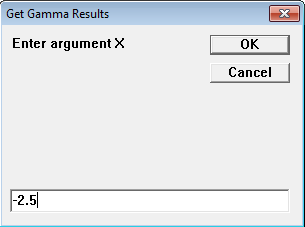
t = INPUTBOX$("Enter argument X", "Get Gamma Results",)
X = VAL(t)
IF X < -1.0 AND ROUND(X, 0) <> X THEN ' X < -1 and non-integer
X1 = ABS(X) + 1.0
s1 = GammLn(X1)
s3 = PI / (EXP(s1) * SIN(PI * X1)) ' Gamma
IF s3 > 0.0 THEN s1 = LOG(s3) ELSE s1 = 1000.0 ' Ln of Gamma
X1 = X1 - 1.0
s2 = GammLn(X1)
s4 = PI / (EXP(s2) * SIN(PI * X1)) ' Factorial
IF s4 > 0.0 THEN s2 = LOG(s4) ELSE s2 = 1000.0 ' Ln of Factorial
END IF
IF X > -1.0 AND X < 0.0 THEN
X1 = ABS(X) + 1.0
s1 = GammLn(X1)
s3 = PI / (EXP(s1) * SIN(PI * X1)) ' Gamma
IF s3 > 0.0 THEN s1 = LOG(s3) ELSE s1 = 1000.0 ' Ln of Gamma
X1 = X1 + 1.0
s2 = GammLn(X1) ' Ln of Factorial
s4 = EXP(s2) ' Factorial
END IF
IF X > 0.0 THEN
s1 = GammLn(X) ' Ln of Gamma
s2 = GammLn(X + 1.0) ' Ln of Factorial
IF VAL(t) <= 1753 AND VAL(t) >= -1753 THEN ' max factorial limit
s3 = EXP(s1)
s4 = EXP(s2)
END IF
END IF
IF s3 <> 0.0 AND s4 <> 0.0 THEN
t2 = "Gamma of " + t + " =" + _
num(s3) + $CRLF + $CRLF
t2 = t2 + "Factorial of " + t + " =" + _
num(s4) + $CRLF + $CRLF
ELSE
t2 = t2 + "Gamma and Factorial: overflow." + _
$CRLF + $CRLF
END IF
IF s1 <> 1000.0 THEN t2 = t2 + _
"Ln of Gamma of " + t + " =" + num(s1) + $CRLF + $CRLF
IF s2 <> 1000.0 THEN t2 = t2 + "Ln of Factorial of " + _
t + " =" + num(s2)
IF X <=-1.0 AND ROUND(X, 0) = X THEN ' X <= -1 and integer
IF X = -1.0 THEN
t2 = "Gamma not defined for X = -1" + _
$CRLF + $CRLF + "Factorial of -1 = 1"
ELSE
t2 = "Gamma and Factorial not defined for X = " + t
END IF
END IF
MSGBOX t2, , "Gamma Function Results:"
END FUNCTION
'
FUNCTION num(BYVAL v AS EXT) AS STRING
IF ABS(v) < 10000.0 AND ABS(v) > 0.0001 THEN
FUNCTION = FORMAT$(v, "#####.################")
ELSE
FUNCTION = FORMAT$(v," 0.################E-####")
END IF
END FUNCTION
[/code]
