11. META-ANALYSIS
The term is derived from the Greek word meta, which means “after”, or “beyond”, so Meta-analysis means a “post-analysis” or summary analysis. It is a scientific method that critically evaluates and statistically combines scientific results from a collection of results to a summary result.
Traditional summary articles are often inadequate: Frequently they do not include all the studies – due to a lack of systematic literature search, selective inclusion criteria, or incorrect compilation of the results. They often reflect the author’s personal experience, knowledge, opinion, attitude, and possible relation to the pharmaceutical industry.
In recent years, the number of meta-analyses has increased significantly, and meta-analyses are included as an important assessment of the evidence for the effects of different treatments. The randomized clinical trial (RCT) is the best way to compare treatment effects, but results from several RCTs can be combined using meta-analysis. Meta-analyses are now performed using more objective criteria and methods to detect bias.
The advantages of a meta-analysis are:
- more objective evidence,
- the possibility of false-negative results is reduced,
- testing of a priori hypotheses concerning the effect in subgroups,
- heterogeneity between the studies can be evaluated and possibly explained.
The downsides are:
- meta-analyzes are not always consistent with large RCTs
- they produce an “average effect”, which may not necessarily be applied to the individual patient,
- they are still sensitive to publication and language bias.
The justification of meta-analyses is that RCTs comparing the same treatments in the same type of patients often will give different results. Two characteristic situations can occur:
- The studies do not show any significant therapeutic effect, but the confidence limits are so wide that a clinically significant treatment effect cannot be ruled out; if the results of the studies could be combined, the treatment effect might be significant.
- Some studies show a treatment effect, others do not. The overall conclusion is therefore uncertain.
Therefore it will often be desirable to combine the results from several uniform studies in a meta-analysis in order to get a more accurate estimate of the treatment effect. Most frequently the analysis has to be based on the summary results from each study, but access to the original data, i.e. the individual patient data, would always be preferable.
There are a number of requirements that must be met for a meta-analysis to provide a credible result:
- Only randomized studies should be included, i.e. all RCTs investigating the treatment in question in the same type of patients must be obtained. Positive results tend to be published more frequently than negative results. So, in order to minimize publication bias, both published and unpublished studies should be included as far as possible,
- Careful research should be carried out to ensure that only truly randomized studies with similar treatment and control groups should be included. The patients, the treatment regimens, and the presentation of results should be comparable in the studies.
Principles in meta-analysis
The treatment groups are compared only within the individual RCT, each RCT is analyzed separately, the same summary statistic is calculated for each RCT, and these summary statistics are then combined in one statistical test that gives the final result.
Binary effect variable
For a binary effect variable, for example, a duodenal ulcer healed or not healed, the result in a single RCT can be summarized in a 2 × 2 table. From these numbers one can calculate these parameters:
Odds ratio = Odds of response in the treatment group divided by the odds of response in control group = (a/b) / (c/d) = (a×d) / (b×c),
If the treatment leads to more response than in the control group, the odds ratio will be above one. If conversely, the treatment leads to less response than in the control group, the odds ratio will be below one.
Relative risk = Risk of response in treatment group divided by the risk of response in control group = (a / (a + b)) / (c / (c + d)),
Risk difference = Risk of response in treatment group minus risk of response in control group = a / (a + b) – c / (c + d).
If the treatment leads to more response than in the control group, the relative risk will be above one and the risk difference will be positive. Then the Number Needed to Treat (NNT) to benefit one patient is 1 divided by the risk difference = 1 / (a / (a + b) – c / (c + d)).
If the treatment leads to less response than in the control group, the relative risk will be below one and the risk difference will be negative. Then the Number Needed to Treat (NNT) to harm one patient is -1 divided by the risk difference = -1 / (a / (a + b) – c / (c + d)).
The difference between odds and risks is that odds relate the number of times the response occurred to the number of times the response did not occur, while risks relate the number of times the response occurred to the number of times the response could have occurred.
Compute Online
Here you can calculate the Odds-Ratio with 95% confidence interval.
Here you can calculate the Relative Risk with 95% confidence interval and the Number Needed to Treat (NNT).
Continuous effect variables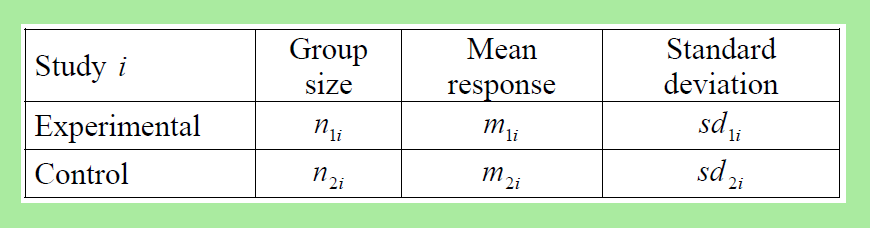
Continuous effect variables are summarized for each RCT as the weighted or standardized mean difference in treatment effect between treatment and control groups.
The mean difference is used when the effect variable has been measured in the same way in each RCT. The result will be in the natural units.
The standardized mean difference is used when the effect variable has been measured differently in each RCT. After the analysis, the result should be transformed back to the natural units.
Sources of heterogeneity in meta-analyses
There may be differences in treatment, assessment of treatment effect, disease criteria, and disease population (clinical heterogeneity) and differences with regard to results between the different RCTs, the influence of background variables, and change of results over time due to changed risk (statistical heterogeneity).
Models for meta-analysis
Fixed-effects model
Here’s the assumption is that the true effect of treatment is the same in each RCT or fixed, and the differences between the different RCT results are due only to random factors.
The inverse-variance method of combining data
The inverse-variance (IV) method is a general method to combine data. For binary data, this method can be used to pool log odds ratios, log risk ratios, and risk differences. and for continuous data, it can be used to pool all mean differences and standardized mean differences. In the general formula, the intervention effect estimate is the study’s log odds ratio, log risk ratio, risk difference, mean difference, or standardized mean difference. The individual effect sizes are weighted according to the reciprocal of their variance, which is calculated as the square of the standard error.
Meta-analysis is performed relatively easily for studies comparing 2 treatments in an unpaired parallel-group design and when the effect variable is binary, for example. +/- response or dead/alive.
The result of a meta-analysis can be illustrated using a Forest plot.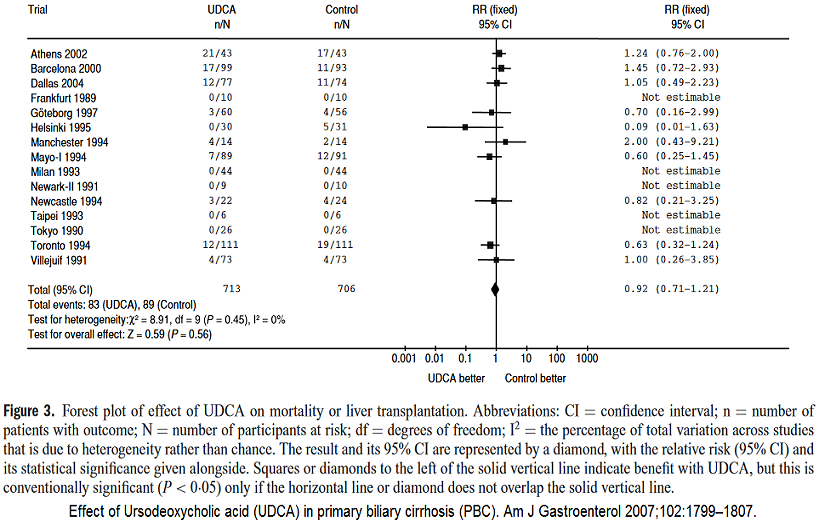
The results for each study are listed in a 2 × 2 table as mentioned above. Meta-analysis is always stratified since each study constitutes a stratum. The result from each 2 x 2 table is included as an independent contribution to the analysis. In this way, one adjusts for the influence of different levels of response in individual studies. Thus it is not correct to make a simple addition (cell for cell) of all 2 × 2 tables into a single 2 × 2 table and then do the analysis on that table.
The fixed-effects model assumes that the odds ratio for the various studies in the analysis is to some extent of similar magnitude. If there is significant heterogeneity in the results one cannot use a fixed-effects method.
Instead, a random-effects model (see below) or more special optional multivariate methods (meta-regression analysis) should be used.
Random-effects model
This model assumes that each RCT shows different true effects, that the effect in the individual RCT usually varies around an overall true average treatment effect, and that the cause of the differences in effect between individual RCTs and the overall true general average effect partly is the real difference between the true effects in the different RCT and partly are random factors.
The random-effects model is used when the results are statistically heterogeneous, i.e. when the results are different and possibly point in opposite directions. A test for statistical heterogeneity must always be carried out. A more complex estimate is calculated for the weighted average effect. This method always provides a more conservative estimate of the treatment effect than the fixed-effects model.
Which method to use in a given meta-analysis must be determined in advance from the nature of the data and the degree of heterogeneity. The chosen analysis method must not be selected on the basis of the results obtained.
If you suspect that certain variables may affect the treatment effect you can perform so-called sensitivity analyses where you compare the treatment effect in subgroups (strata) defined by that variable. It will often be reasonable to perform sensitivity analyzes using strata defined by important prognostic variables. If the results of these sensitivity analyzes are stable, one can say that the meta-analysis result is robust. A more detailed analysis of the influence of background variables can be done using meta-regression analysis.
A meta-analysis based on individual patient data
If you have access to individual patient data, it will be possible to perform a more complete meta-analysis, which takes into account the influence of important patient characteristics – or background variables – that may influence the effect. In some cases, there may be an interaction between the effect of the treatment and the prognostic variables. This can only be investigated by analysis of individual patient data.
Unfortunately, it is rare for individual patient data to be available from all studies. Therefore result in meta-analyses based on individual patient data may be affected by an RCT selection bias.
Bias in meta-analysis
Bias may occur in meta-analyzes and may be due to publication bias, due to positive RCTs being published more frequently than negative RCTs, poor methodological quality in smaller RCTs, true heterogeneity, random factors, and possibly fraud.
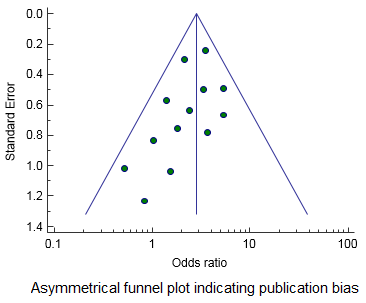A funnel plot is a graphical tool for detecting bias in meta-analysis. In a funnel plot, the treatment effect is plotted on the horizontal axis and the standard error on the vertical axis. The vertical line represents the summary estimated derived using a fixed-effect meta-analysis. The two diagonal lines represent 95% confidence limits (effect ± 1.96 SE) around the summary effect for each standard error on the vertical axis. In the absence of heterogeneity, 95% of the studies should lie within the funnel defined by these diagonal lines.
A bias will result in an asymmetry of the funnel plot. If publication bias is present, the smaller studies will show the larger effects. This will produce an asymmetric funnel plot as shown in the figure to the left.
Meta-Analysis Program
I have made a program, which you can use to make your own meta-analyses: Meta-Analysis Program by ECstep.
