5. Sample Size Determination
4.38/5 (8)
In planning a study, for example, a controlled clinical trial, it is necessary to calculate the necessary number of subjects to be included to ensure that the study can give an unambiguous result: either a significant difference (p-value <2α ⇒ null hypothesis rejected) or – if the result is negative (p-value> 2α ⇒ null hypothesis not rejected) – a low probability (small type 2 error risk) of a false negative result that overlooks a significant difference.
If the calculation shows that a given study would require more individuals than it is possible to include, then the study should not be performed because it is unethical and a waste of resources to perform studies, which cannot give a clear result.
The null hypothesis means no difference between the groups. The alternative hypothesis would be that there is a difference between the groups. No matter how big a trial is being planned, there will always be a limit to how small differences it will be able to demonstrate.
–
–
Comparison of means in two independent groups
Prior to calculating the required number of subjects one must specify the minimal relevant difference Δ (effect size) that the trial should be able to find if it exists. The level of significance (2α) and the power (1 – β) should be specified by the examiner and be based on biological knowledge and clinical experience, i.e. the balance between the benefits of demonstrating a true difference and the risk of finding a false difference.
Finally, in order to calculate the required number of subjects in each treatment group (N) one should know the variance (S²) of the difference that you want to evaluate. The calculation is made according to formula 5.1.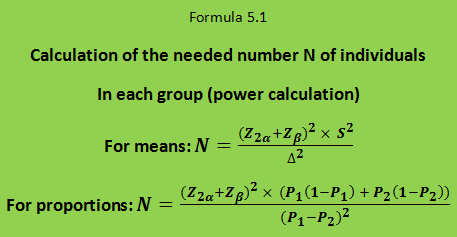
The Z-values are not in all situations equal to the standard normal deviate. Calculation of the required number of individuals will not be exact, but usually, one will only commit an unimportant error in assuming that the Z-values are standard normal deviates. In a study with two independent groups, a total of 2N individuals would be needed. In a paired study, there is only one group, as each patient will receive both the one and the other treatment in random order.
The variance of the effect variable is often known from previous studies. Otherwise, it may be estimated in a pilot experiment.
For normally distributed variables the variance of the difference between two independent measurements (S²) is the sum of the variance of the first measurement (S1²) and the variance of the second measurement (S2²), i.e. S² = S1² + S2².
For an unpaired trial with two independent groups studying a normally distributed effect variable, the variance S² of the difference (in formula 5.1) is twice as large as the variance of the effect variable, which typically will be known from previous studies, i.e., S² = 2 × S1².
Example: A researcher wants an unpaired design with two groups to test a new cholesterol-lowering agent. The effect variable is the concentration of cholesterol in serum. You want to plan an experiment in which there is an 80% chance to detect a significant effect of the drug at the 5% level if the new drug lowers serum cholesterol by 0.8 mmol/l more than the control treatment. That is 1 – β = 80% ⇒ β = 20% ⇒ Zβ = 0.84; 2α = 5% ⇒ Z2α = 1.96; Δ = 0.8 mmol / l. In a pilot experiment, the standard deviation of serum cholesterol was estimated to be 1.2 mmol/l in such patients. Then the number of subjects needed could be calculated: N = (1.96 + 0.84)² × 2 × 1.2² / 0.82 = 36 persons in each treatment group, i.e. a total of 72 patients.
Comparison of paired means
If the variation in serum cholesterol levels between patients is higher than for repeated measurements in the same patient, and if the same study could be performed in a paired design (as a cross-over trial), a much smaller number of patients would be needed. For a paired trial S² corresponds to the variance of the difference Sdif² between two measurements (one for each treatment) in the same person, i.e. the so-called intra-individual variance, which depends on the correlation coefficient of the paired measurements; this equation can be used: Sdif² = 2 × S² × (1 – r).
Example: The above study is being planned as a paired cross-over trial. Δ, 2α, β and S² are unchanged. The coefficient of correlation r between successive cholesterol levels in each patient was found to be 0.625. The variance of the intra-individual difference was obtained using the equation: Sdif² = 2 × S² × (1 – r) = 2 × 1.2² × 0.375 = 1.08. Then N = (1.96 + 0.84)² × 1.08 ⁄ 0.8² = 13.3. Thus only 14 patients will be needed in this one group study. That is less than ¼ of the number needed for the two groups’ study.
Often one comes across the term “power calculation” to describe the above calculation of the required number of individuals. This term is strictly spoken misleading because β and thus the power (1 – β) – like 2α and Δ – are not calculated but specified by the investigator as a prerequisite for the calculation.
After the trial is completed, a so-called post hoc power calculation would rarely be meaningful, since 2α now has been realized to the p-value obtained from the statistical test. Also, the result obtained in the study would be a factual estimate of the difference in effect between the two treatments. Therefore, the calculation of the confidence interval for the observed difference would be the best description of the precision of the result. The confidence interval would also be the appropriate starting point to calculate the probabilities that the real difference is greater than or less than the specified Δ-value.
–
–
Comparison of two independent proportions
If the effect variable is a proportion the variance becomes P1 (1 – P1) + P2 (1 – P2) where P1 and P2 are the expected proportion of respondents in the two groups. Δ becomes P1 – P2, see formula 5.1 for proportions.
Example: The response of the traditional treatment in a given disease is 50%, and one expects the new treatment to give a response in 70% of the individuals. Provided that the expectation for the new treatment is correct, we want to plan an experiment which has 80% probability to show that the new treatment is better than the old one with a significance level of 5%; i.e. P1 = 0.5; P2 = 0.7; Δ = P1 – P2 = 0.2; 2α = 0.05 ⇒ Z2α = 1.96; β = 0.20 ⇒ Zβ = 0.84. The required number of subjects N in each group is calculated by formula 5.1 for proportions: N = (1.96 + 0.84)² × (0.5 × 0.5 + 0.7 × 0.3) / 0.2² = 90.2, i.e. 91 patients in each group and 182 patients in total.
Compute online
Using this link you can calculate the sample size for comparing two means (averages) and the sample size for comparing two proportions (percentages). Here is another link to a slightly more advanced page where you can also calculate the minimal relevant difference (effect size) that can be detected if you know the number of individuals in advance. You can also calculate sample size for correlation coefficients and non-inferiority trials. For reference here is a link to my paper on equivalence and non-inferiority trials.


