7. Survival Analysis
4.67/5 (6)
Survival analysis is used to analyze survival times in groups of subjects.
Everything develops and progresses in time. In medicine, a description of the course in time is an important aspect in the characterization of diseases, including their prognosis and the effects of therapies. However, a detailed description of the course of the disease may be complex.
 Accordingly, the problem has been dealt with in simpler terms, namely by analyzing for each individual the time from a defined starting point, e.g., the time of diagnosis or randomization in a controlled clinical trial to the occurrence of an event or endpoint of interest, traditionally death as in survival analysis.
Accordingly, the problem has been dealt with in simpler terms, namely by analyzing for each individual the time from a defined starting point, e.g., the time of diagnosis or randomization in a controlled clinical trial to the occurrence of an event or endpoint of interest, traditionally death as in survival analysis.
In principle, the first occurrence of other events such as complications. freedom of symptoms, recurrence of symptoms, etc., may be defined as an endpoint for the subject and analyzed in a similar way, although the precise registration of the time at which the event takes place may be difficult.
Since investigations have a limited duration, some subjects may not yet have had the event, but are still “alive” at the end of the investigation. Other subjects, while alive, may have dropped out for various reasons during the study without the event having occurred.
Such “incomplete” survival times from the starting point to the latest observation, so-called censored survival times, which hold the information that the event did not occur while the individual was being observed, are utilized along with the “complete” survival times in the analysis of survival data.
Table 1 presents a constructed set of survival data that will be used for illustration. The data set includes 30 subjects, of whom 18 have a complete observation time with an endpoint, and 12 have a censored observation time without an endpoint.
The values of the variables presented (albumin, bilirubin, and alcoholism) apply to the beginning of the follow-up period.
–
–
THE SURVIVAL CURVE
The established way of presenting survival data is to estimate the survival curve. If all of the survival times are complete, i.e., without censoring, the survival curve is estimated simply as the proportion of individuals in whom the event has not yet occurred at each point of time during the observation period.
 For survival data which includes censored survival times, the survival curve may be estimated by a method described by Kaplan and Meier. By including the censored survival times, that method gives a useful estimate of the probability of not having the event (i.e., to survive) as a function of time.
For survival data which includes censored survival times, the survival curve may be estimated by a method described by Kaplan and Meier. By including the censored survival times, that method gives a useful estimate of the probability of not having the event (i.e., to survive) as a function of time.
Since this probability is a function of the probability of surviving all time intervals from start to a given time t it is denoted the cumulative survival probability – commonly designated S(t).
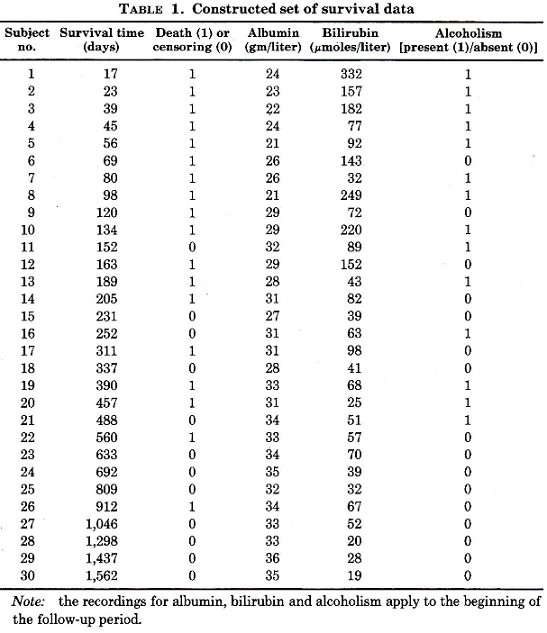
The estimated cumulative survival probability curve S(t) for the total group of individuals presented in Table 1 is shown in Figure 1 (top panel).
Compute online
Here you can compute the Kaplan Meier survival plot online. Here is an alternative link that also calculates the log-rank test (see below). Here is a third link where you can type or copy/paste data, or read it in from a file. Prepares tables, graphs (with 95% confidence intervals), and statistical comparison output. Can accommodate two or more groups, and can perform a stratified log-rank test (see below). Provides a high-quality output.
–
–
HAZARD
The more recent methods for the analysis of survival data including Cox regression analysis are based on the instantaneous hazard (also called the force of mortality) designated λ(t), which is the risk that the event will occur for a subject in a small time interval (Δt) at time t, given the subject did not have the event before that time.
Since the hazard λ(t) is the derivative of the cumulative (integrated) hazard designated Λ(t), it can be illustrated by the slope of the latter. Using the relation Λ(t) = -ln(S(t)), the cumulative hazard may easily be estimated by taking the negative natural logarithm of the corresponding cumulative survival probability estimates S(t).
The estimated cumulative hazard curve Λ(t) of the survival data in Table 1 is shown in the bottom panel of Figure 1. A steep rise in that curve corresponds to a high hazard, a slight rise to a low hazard. It appears from the curve that the hazard is high initially and less thereafter.
A cumulative survival curve and the cumulative hazard curve derived from it are summarizing descriptions concerning the studied total group of individuals. However, there may be a wide variation in the survival time (and hazard) between individual subjects.
Although the curves illustrate the variation among the subjects, they do not allow identification of who had a long survival (low hazard) and who had a short survival (high hazard).
COVARIATES – VARIABLES
To allow the prediction of survival time in individual subjects, it is necessary to identify and utilize variables covarying with survival.
For example, it may be that serum albumin at the starting point covaries with the subsequent survival time; i.e., in subjects with low albumin, the survival time may be short (hazard high), and in subjects with high albumin, the survival time may be long (hazard low).
If the covariation (or correlation) between the level of albumin and the survival time is large, the level of albumin may to some degree “explain” the variation in survival time or hazard between the subjects. In that case, the level of serum albumin in a new subject may to some degree be used to predict his/her survival time or hazard.
In a controlled clinical trial, the treatment given may be an important covariate that may “explain” a difference in survival between the treatment groups.
–
–
COMPARISON OF SUBGROUPS (STRATA) – THE LOGRANK TEST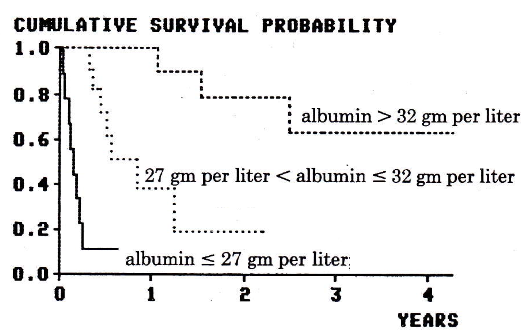
The simplest way to identify prognostic covariates is to divide the subjects in subgroups (strata) according to different levels of a given variable.
For example, if we divide the subjects presented in Table 1 according to the level of albumin (e.g., albumin <28, 28 to 32, and >32 gram per liter), it can be shown in Figure 2 that the survival curves for these three groups are markedly different.
You can use the statistical logrank test to compare the survival curves of two or more groups.
In a similar way, one can show for the subjects presented in Table 1 that the survival curves are different in subgroups defined according to the level of bilirubin or the presence or absence of alcoholism.
Normally, a single variable, even if it shows a strong covariation with survival, will not completely “explain” survival. Usually, it is to be expected that more variables in combination may “explain” survival to a higher degree.
It is possible to stratify according to more than one variable at a time. However, with an increasing number of strata, the number of subjects in each stratum will rapidly decrease to such an extent that the corresponding survival curves will have too little “confidence” [the curves will have too wide confidence limits] to be of any value.
Hence, in practice, stratified analyses can only be performed with one or few variables at a time. This puts a serious limitation on stratification. However, the method may be used for a crude screening to identify variables that should be analyzed further in a Cox regression model.
Compute Online
Using this link you can calculate the logrank test online. This link also provides the cumulative survival curves estimated by the Kaplan-Meier method. Here is a second link where you can type or copy/paste data, or read it in from a file. Prepares tables, graphs (with 95% confidence intervals), and statistical comparison output. Can accommodate two or more groups, and can perform a stratified log-rank test. Provides a high-quality output.
–
–
COX REGRESSION MODEL
The regression model proposed by Cox is a multiple regression model for the analysis of censored survival data. I have written an article about the Cox model here. Provided that the more strict assumptions (described later) of this model may be considered fulfilled, it may be used to study and utilize the pattern of covariation of many variables with the hazard.
The Cox regression model has this form
λ(t, z) = λ0(t) exp(b1z1 + … + bizi + … + bpzp).
Thus λ(t, z), the hazard at time t after a defined starting point [diagnosis, randomization, etc. (being time zero)] for an individual with variables z (z1. . .zi. . .zp) is being “dependent on” or “explained” or “predicted” by λ0(t), the so-called underlying hazard at time t, and the predictor variables z1 to zp (recorded at time zero), each variable zi being multiplied by a corresponding regression coefficient bi.
Here, exp stands for the exponential function. The underlying hazard λ0(t) may be considered a “reference” hazard from which the hazard λ(t, z) at time t of a given subject may be obtained by multiplication with a factor, namely the exponential function of the subject’s variables “weighted” by the regression coefficients.
Formally, the underlying hazard λ0(t) is the hazard at time t of an individual whose z’s are all zero. Usually, λ0(t) is of little interest in itself, since it may depend on the scoring of the variables.
Thus, the Cox model assumes that the hazards of any two patients are proportional over time, i.e., the ratio between the hazards is the same at any time t. This does not preclude that the hazard may change over time. Often, the hazard will be relatively high soon after the time of diagnosis and thereafter it may decrease as in Figure 1.
However, the Cox model assumes that changes in the hazard of any patient over time will always be proportional to changes in the hazard of any other patient and to changes in the underlying hazard over time.
The amount by which each predictor variable zi contributes to the prediction of the hazard λ(t, z) of an individual depends on the magnitude of the corresponding term bizi. If the term is numerically big, then the contribution is big; if the term is numerically small (close to zero), then the contribution is small.
FITTING A COX MODEL TO A SET OF DATA
The estimation of the b coefficients and the underlying hazard in the Cox regression model is complex. The statistical and computational details are described in the literature. However, to perform Cox analyses using available standard computer programs (see later data), knowledge of these details is not necessary.
The procedure is illustrated by performing a Cox regression analysis on the data presented in Table 1. In the analysis, serum albumin will be scored by its value in grams per liter and alcoholism as 1 if present and 0 if absent.
Serum bilirubin will be scored by log10 of the values in μmoles per liter as in a previously published study. For example, if serum bilirubin is 92 μmoles per liter, it will be scored as 1.98227 . . . . Later, it will be shown if this scoring is adequate.
As in simple multiple regression analysis, variables may be selected according to certain procedures (forward selection or backward elimination).
To illustrate how this works (the details will be explained in the following),  Table 2 presents the results of seven Cox analyses comprising all possible combinations of the three variables in Table 1, i.e., three including only one variable (Models 1 to 3), three including two variables (Models 4 to 6) and one including all three variables (Model 7).
Table 2 presents the results of seven Cox analyses comprising all possible combinations of the three variables in Table 1, i.e., three including only one variable (Models 1 to 3), three including two variables (Models 4 to 6) and one including all three variables (Model 7).
OVERALL SIGNIFICANCE OF THE MODEL (LIKELIHOOD RATIO TEST)
Estimation and significance testing of a given Cox model involves the concept of likelihood, meaning the probability of the observed data being “explained” by a certain model.
The overall significance of each model shown in Table 2 is based on the ratio between the likelihood of a model in which the variables show no covariation with the survival time, the b coefficients all being zero, L(0), and the likelihood of the model with the b coefficient(s) obtained by the analysis, L(b), the b coefficient(s) being estimated in such a way that L(b) is as great as possible.
Thus, the estimated parameters (the underlying hazard and the coefficients) of a Cox model are so-called “maximum likelihood estimates”. The greater the L(b) or the less the likelihood ratio L(0)/L(b), the better the model actually “explains” or fits the observed data.
The significance of each model can be tested statistically using the relation: χ²model = 2 × [ln(L(b)) – ln(L(0)] with degrees of freedom (d.f.) being equal to the number of coefficients estimated in the model. While ln(L(0)) is the same for all of the models, i.e., -52.319, L(b) and hence the χ²model depend on the variable(s) included.
For example, for Model 1, ln(L(b)) is -36.825, and the χ²model becomes 30.99 as shown in Table 2. This high χ² value with 1 d.f. is highly significant.
Considering the three models in Table 1, including only one variable (Models 1 to 3), it appears that the highest χ²model is provided by Model 1, which therefore has the greatest significance of those three models.
–
–
SIGNIFICANCE OF EACH INCLUDED VARIABLE
For each variable in each analysis, Table 2 presents the regression coefficient b and the standard error of b [SE(b)], which indicates the “confidence” of the estimated b value and may be used to estimate the confidence limits of b.
As shown in the table, the significance of each coefficient can be estimated by comparing the normal deviate, N.D. = b/SE(b), with the standard normal distribution.
Identical results are obtained by comparing the square of the normal deviate, i.e., N.D.² with the χ²-distribution with 1 d.f. (the so-called Wald test [sometimes presented in computer printouts]).
The relative importance of the variables is given by the numerical value of N.D. The greater the numerical value of N.D., the more significant it is in the model. Considering Model 7 in Table 2, the importance of the variables decreases in this order: albumin, log10(bilirubin), and alcoholism (the latter being insignificant).
–
–
SELECTION OF VARIABLES
With the forward selection method, the model is built up step-wise by including at each step the variable giving the largest increase in the χ² model.
Thus, in the first step, albumin (Model 1 in Table 2) would be included because this variable gives the highest significant χ² model of all possible models with one variable (Models 1 to 3).
In the next step, log10 bilirubin would be added (Model 4) because this variable increases the χ² model significantly (4.90 with 1 d.f., p < 0.05) in contrast to alcoholism (Model 5), which only gives an insignificant increase in the χ²model (1.51 with 1 d.f., p > 0.2). (Here, d.f. is the difference between the number of estimated coefficients in the models being compared.)
The inclusion of alcoholism in a model comprising albumin and log10 bilirubin (Model 7) does not lead to a significant increase in the χ² model (1.15 with 1 d.f., p > 0.2). Therefore, Model 4 would be the final model if the forward inclusion technique was used.
Utilizing the backward elimination method, one starts with a model which includes all variables, and then insignificant variables are removed step-wise from the model by excluding the most insignificant variable at each step until each remaining variable contributes significantly to the model.
Thus, one would start with Model 7 and then remove alcoholism because this variable is insignificant. This would lead to Model 4, which would be the final model because both variables (albumin and log10 bilirubin) are statistically significant.
For the data in Table 1, forward selection and backward elimination of variables lead to the same final model. In more complex analyses, including many variables, the two methods of selection of variables may lead to slightly different final models.
Normally, the selection of variables should not be made solely according to automatic rules. The selection process should be guided by the investigator by taking into account, among other things, the a priori prognostic value of each variable considered.
INFLUENCE OF COVARIATION BETWEEN PREDICTOR VARIABLES
In general, the pattern of covariation between the predictor variables will, to some extent, determine which will be significant in the final Cox regression model.
It is not always possible from the results of univariate analyses (including only one variable, e.g., Models 1 to 3 in Table 2) to predict which variables will be significant in a Cox regression model, including more variables.
If two variables, each of which has shown a significant covariation with survival time by univariate analysis, are strongly intercorrelated, and therefore holding nearly the same information, only one of them may be significant if both are included in the model.
On the other hand, a variable that has shown no significant covariation with survival if included as the only variable may be significant if included together with other variables.
The reason for this is that multivariate – in contrast to univariate – statistical analyses can adjust for the influence (covariation) of other variables with the variable in question.
Furthermore, the magnitude of the regression coefficient and the degree of significance of each included variable depend on which other variables are also included in the model as shown in Table 2.
For example, by comparing Models 3 and 5, it appears that alcoholism is significant if it is the only variable in the model (Model 3); but if albumin is also included (Model 5), the influence of alcoholism is no longer significant.
Furthermore, the value of the b coefficients changes from the models including one variable to the model having both variables [b for albumin changes from -0.42 (Model 1) to -0.39 (Model 5) and b for alcoholism changes from 1.55 (Model 3) to 0.79 (Model 5)].
The reason for these differences is the covariation between the predictor variables (in this case between albumin and alcoholism). This covariation is adjusted for in the Cox model so that only the independent association of each variable with the hazard is presented in the estimated model.
If, however, the covariation between two or more predictor variables is very strong (collinearity), the estimated regression coefficients may be affected so much that the results may no longer be interpreted in a simple meaningful way. The solution will often be to include in the model only one variable from the highly correlated set.
Compute online
Here is a link to a site performing a Cox regression analysis: You should specify each subject’s observation time and status (last seen alive or dead), and any number of independent variables (predictors, confounders, and other covariates). This web page will perform proportional-hazards regression analysis and return the regression coefficients, their standard errors, hazard (risk) ratio, their confidence intervals, and the baseline survivor curve, along with goodness-of-fit information.
Here is a link to another site performing a Cox regression analysis: You can copy/paste data from Excel, or upload a CSV file. Produces a regression table report, survival plot, survival table, log-rank test, and a predicted survival plot for specified covariable patterns. Provides a high-quality output.


