Matrix Inversion
Matrix inversion is often performed to simplify solving a system of linear equations.
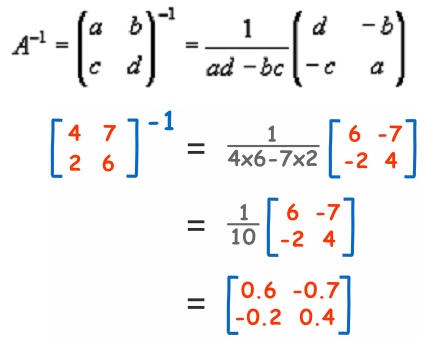To invert a matrix it must be square i.e. have the same number of rows and columns, and the so-called determinant should not be zero.
If a square matrix has an inverse it is called invertible, otherwise, it is called singular.
The source code presents two versions of matrix inversion. SUB MatInvers is the simplest version, which illustrates how matrix inversion is done.
SUB MatInversRCI is designed to maintain the highest possible precision in the calculations. Both versions use Gaussian elimination and both calculate the determinant.
[code language="vb"]
#COMPILE EXE
#DIM ALL
'
FUNCTION PBMAIN
LOCAL I, J, M AS LONG
M = 3 ' number of rows and columns in matrix
DIM ma(1 TO M, 1 TO M) AS EXT ' extended precision
LOCAL Det AS EXT, T AS STRING
' matrix
ma(1,1) = 1.0 : ma(1,2) = 3.0 : ma(1,3) = -4.0
ma(2,1) = 5.0 : ma(2,2) = 2.0 : ma(2,3) = 1.0
ma(3,1) = 3.0 : ma(3,2) = 2.0 : ma(3,3) = -2.0
Det = 1.0
CALL Results(ma(), M, Det, T, "Original")
' CALL MatInvers(ma(), M, Det)
CALL MatInversRCI(ma(), M, Det)
CALL Results(ma(), M, Det, T, "Inverted")
' CALL MatInvers(ma(), M, Det)
CALL MatInversRCI(ma(), M, Det)
CALL Results(ma(), M, Det, T, "Inversion of inverted matrix = Original")
MSGBOX T ,,"Results:"
END FUNCTION
'
SUB MatInvers(BYREF A() AS EXT, BYVAL M AS LONG, BYREF Det AS EXT)
' Gauss reduction inversion method.
' M is the order of the square matrix A()
' A() inverse is returned in A().
' Determinant is returned.
LOCAL I, J, K, L AS LONG, Te AS EXT, Pivot AS EXT
Det = 1.0
FOR J = 1 TO M
Pivot = A(J,J) : A(J,J) = 1.0
Det = Det * Pivot
IF Det = 0.0 THEN
MSGBOX "Matrix singular - cannot invert",,"Problem": EXIT SUB
END IF
' Divide pivot row with pivot element.
FOR K = 1 TO M : A(J,K) = A(J,K) / Pivot : NEXT
FOR K = 1 TO M
' Reduce the non pivot rows.
IF K <> J THEN
Te = A(K,J) : A(K,J) = 0.0
FOR L = 1 TO M : A(K,L) = A(K,L) - A(J,L) * Te : NEXT
END IF
NEXT
NEXT
END SUB
'
SUB MatInversRCI(BYREF A() AS EXT, BYVAL M AS LONG, BYREF Det AS EXT)
' calculate inverse and determinant by the Gauss-Jordan method
' M is the order of the square matrix A()
' A() inverse is returned in A().
' Determinant is returned.
' This version brings the largest elements of the matrix
' to the diagonal to serve as pivot divisors.
' This is done by interchanging rows and columns. In this
' way you avoid losing precision, which could have occured by
' dividing very large numbers by very small numbers.
LOCAL I, J, K, L, L1, Irow, Icol AS LONG, Amax, SW AS EXT
DIM Ipvt(1 TO M) AS LOCAL LONG, Pvt(1 TO M) AS LOCAL EXT
DIM indx(1 TO M, 1 TO 2) AS LOCAL LONG
Det = 1.0
FOR J = 1 TO M : Ipvt(J) = 0 : NEXT
FOR I = 1 TO M
' search for the pivot element
Amax = 0.0
FOR J = 1 TO M
IF Ipvt(J) <> 1 THEN
FOR K = 1 TO M
IF Ipvt(K) <> 1 THEN
IF ABS(Amax) < ABS(A(J, K)) THEN
Irow = J
Icol = K
Amax = A(J, K)
END IF
END IF
NEXT
END IF
NEXT
INCR Ipvt(Icol)
' interchange the rows to put pivot element on the diagonal
IF Irow <> Icol THEN
Det = -Det
FOR L = 1 TO M
SWAP A(Irow, L), A(Icol, L)
NEXT
END IF
Indx(I, 1) = Irow : Indx(I, 2) = Icol
Pvt(I) = A(Icol, Icol)
Det = Det * Pvt(I)
A(Icol, Icol) = 1.0
IF Det = 0.0 THEN
MSGBOX "Matrix singular - cannot invert",,"Problem"
EXIT SUB
END IF
' divide the pivot row by the pivot element
FOR L = 1 TO M
A(Icol, L) = A(Icol, L) / Pvt(I)
NEXT
' reduce non-pivot rows
FOR L1 = 1 TO M
IF L1 <> Icol THEN
SW = A(L1, Icol)
A(L1, Icol) = 0.0
FOR L = 1 TO M
A(L1, L) = A(L1, L) - A(Icol, L) * SW
NEXT
END IF
NEXT
NEXT
' interchange the columns
FOR I = 1 TO M
L = M + 1 - I
IF indx(L, 1) <> indx(L, 2) THEN
Irow = indx(L, 1)
Icol = indx(L, 2)
FOR K = 1 TO M
SWAP A(K, Irow), A(K, Icol)
NEXT
END IF
NEXT
END SUB
'
SUB Results(BYREF ma() AS EXT,BYVAL M AS LONG, _
BYVAL Det AS EXT, BYREF T AS STRING, BYVAL T2 AS STRING)
LOCAL I AS LONG, J AS LONG
T = T + T2 + " matrix" + $CRLF
IF Det <> 0 THEN
FOR I = 1 TO M
FOR J = 1 TO M
T = T + STR$(ma(I, J), 18) + " "
NEXT
T = T + $CRLF
NEXT
IF Det <> 1 THEN
T = T + "Determinant = " + _
STR$(Det, 18)+$CRLF+$CRLF
ELSE
T = T + $CRLF
END IF
END IF
END SUB
[/code]
