3. Confidence Interval
From sample to population
In the preceding section we have described how means and proportions vary in random samples from a population. What we really want to know is to what degree we may extrapolate the findings in the sample back to the population – or expressed in another way: What can we know about the population based upon the findings in the sample? To answer this we introduce the concept of likelihood and the confidence interval or the confidence limits.
–
The Likelihood Function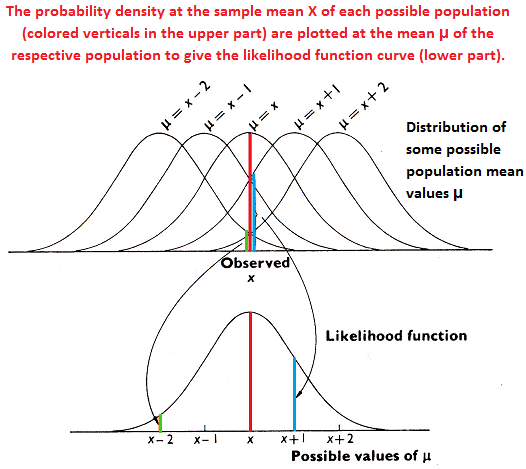
Based on the findings in the sample and the spectrum of populations, that can give rise to such findings, one can construct a distribution of probabilities of the various populations at the sample mean X as shown in the figure to the right. This constructed distribution is called the likelihood function from which one can determine the relative likelihood of the different possible population means μ. Since the likelihood function has a maximum at the sample mean X, that value is considered the best estimate of the population mean μ. Therefore that value is called the maximum likelihood estimate of the population mean μ .
–
The Confidence interval
In practice one would want to know the interval within which the population mean would be with a certain probability. Such an interval is called a confidence interval. The upper and lower limit of the confidence interval are called the confidence limits.
–
Confidence interval of a mean
Assuming that all population means a priori are equally likely, the confidence interval can be derived from the likelihood function, since the area under the curve for a given interval around the sample mean would indicate the likelihood that the population mean lies in the interval.
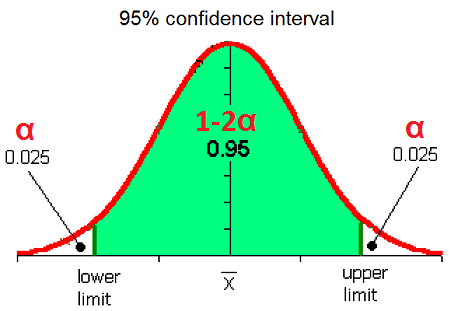
Since the normal distribution is symmetrical, the probability α (alpha) that the population mean lies below the interval would be the same as the probability (=α) that the population mean lies above the interval. Therefore, the probability that the population mean lies within the interval is 1 – 2α.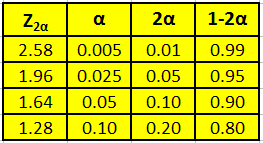
The confidence interval is calculated by using formula 3.1.
Confidence interval of a population mean
In a population of a given size the standard deviation (SD) and hence the standard error of the mean (SEM) have fixed values. This means that we can use the first of the two formula 3.1 and apply the Z-score of the standard normal distribution to calculate the confidence interval. In the yellow table you can see important corresponding values for the Z-score for 2α and the corresponding 1-sided (α) and 2-sided (2α) probabilities as well as 1-2α.
If we want to calculate the 95% confidence interval this would be the mean value ± SEM x 1.96. The 90% confidence interval would be the mean value ± SEM x 1.64, and the 99% confidence interval would be the mean value ± SEM x 2.58.
Confidence interval of a sample mean
In a sample taken from the population both the mean and the standard deviation (and SEM) need to be estimated from the data in the sample. This has the consequence that the probability distribution of the means becomes slightly flatter and broader than the standard normal distribution. This special distribution – termed Student’s t-distribution – depends on the degrees of freedom i.e. the number of values in the final calculation that are free to vary. In this case the degrees of freedom ν = N-1, i.e. the number of individuals (N) in the sample minus one. Here we should use the second of the two formula 3.1. The t-distribution becomes increasingly flatter and broader as the number of individuals in the sample decreases as seen in the figure. A detailed table of Student’s t-distribution is here.
–
Confidence interval of a proportion
An approximate confidence interval of a proportion P can be calculated using formula 3.2. An exact confidence interval is more difficult to calculate because it involves using the binomial distribution. However, if the sample size is large and the proportion is not very small (close to zero) or very large (close to one), the confidence interval obtained using the standard normal distribution is a good approximation.
Compute online
Using this link you can calculate the t-value corresponding to a given probability and the degrees of freedom (use the t ratio line in the link).
Using this link you can calculate 99%, 95% and 90% confidence intervals from the sample mean, sample size and standard deviation.
Here you can calculate exact confidence limits of a proportion using the binomial distribution (you can set the confidence level at the bottom of the link page).
