Beta function
The Beta function is a function of two variables which is often found in probability theory and mathematical statistics. It plays a role in the F- distribution and the Student’s t-distribution.
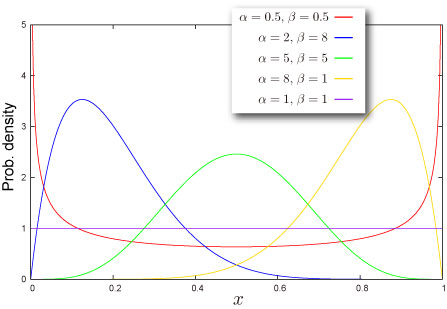The Beta distribution represents a probabilistic distribution of probabilities – the case where we don’t know what a probability is in advance, but we have some reasonable guesses.
The incomplete beta function is a generalization of the beta function.
The cumulative beta distribution is the same as the so-called regularized incomplete beta function. If this is multiplied by the corresponding beta function one obtains the actual incomplete beta function.
The source code estimates the various beta functions. The source code includes the gamma function, which is needed for the estimation.
[code language="vb"]
#COMPILE EXE
#REGISTER NONE
#DIM ALL
'
SUB IncomplBeta(BYVAL X AS EXT, BYVAL P AS EXT, BYVAL Q AS EXT, _
BYREF beta AS EXT, BYREF betain AS EXT)
'
' Derived from FORTRAN code based on:
' algorithm AS 63 Appl. Statist. (1973), vol.22, no.3
' Computes incomplete beta function ratio for arguments
' X between zero and one, p (=a) and q (=b) positive.
' Returns log beta and Regularized Incomplete Beta
'
LOCAL ns, indx AS LONG
LOCAL zero, one, acu AS EXT
LOCAL psq, cx, xx, pp, qq, term, ai, rx, temp AS EXT
' define accuracy and initialise
zero = 0.0 : one = 1.0 : acu = 1.0E-18
betain = 0.0 : beta = 0.0
' test for admissibility of arguments
IF(p <= zero OR q <= zero) THEN EXIT SUB
IF(x < zero OR x > one) THEN EXIT SUB
IF(x = zero OR x = one) THEN EXIT SUB
' calculate log of beta by using function GammLn
beta = gammln(p) + gammln(q) - gammln(p + q)
betain = x
' change tail if necessary
psq = p + q
cx = one - x
IF (p < psq * x) THEN
xx = cx
cx = x
pp = q
qq = p
indx = 1
ELSE
xx = x
pp = p
qq = q
indx = 0
END IF
term = one
ai = one
betain = one
ns = qq + cx * psq
' use Soper's reduction formulae.
rx = xx / cx
temp = qq - ai
IF (ns = 0) THEN rx = xx
DO
term = term * temp * rx / (pp + ai)
betain = betain + term
temp = ABS(term)
IF(temp <= acu AND temp <= acu * betain) THEN EXIT DO
ai = ai + one
ns = ns - 1
IF (ns >= 0) THEN
temp = qq - ai
IF (ns = 0) THEN rx = xx
ELSE
temp = psq
psq = psq + one
END IF
LOOP
' calculate Regularized Incomplete Beta
betain = betain * EXP(pp * LOG(xx) + (qq - one) * LOG(cx) - beta) / pp
IF indx = 1 THEN betain = one - betain
END SUB
FUNCTION PBMAIN
LOCAL i1, i2 AS LONG
LOCAL Result AS STRING
LOCAL X, a, b, Beta, Ibeta AS EXT
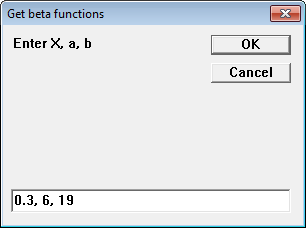
Result = INPUTBOX$("Enter X, a, b","Get beta functions")
i1 = INSTR(Result, ",")
i2 = INSTR(i1 + 1, Result, ",")
X = VAL(LEFT$(Result, i1 - 1))
a = VAL(MID$(Result, i1 + 1, i2 - i1 - 1))
b = VAL(MID$(Result, i2 + 1))
CALL IncomplBeta(X, a, b, Beta, Ibeta)
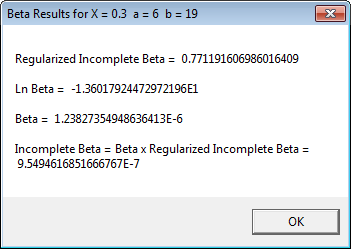
Result = "Regularized Incomplete Beta = " + _
FORMAT$(Ibeta," 0.##################") + _
$CRLF + $CRLF + "Ln Beta = " + _
FORMAT$(Beta," 0.##################E-####") + _
$CRLF + $CRLF + "Beta = " + _
FORMAT$((EXP(Beta))," 0.##################E-####") + $CRLF + $CRLF + _
"Incomplete Beta = Beta x Regularized Incomplete Beta =" + $CRLF + _
FORMAT$((EXP(Beta)*Ibeta)," 0.##################E-####")
MSGBOX Result, , "Beta Results for X = "+FORMAT$(X,"0.#####") + _
" a ="+STR$(a) + " b ="+STR$(b)
END FUNCTION
'
FUNCTION GammLn(BYVAL x AS EXT) AS EXT
' Returns Ln(Gamma()) or 0 on error
' Based on Numerical Recipes gamma.h
' Lanczos, C. 1964, "A Precision Approximation
' of the Gamma Function," SIAM Journal on Numerical
' Analysis, ser. B, vol. 1, pp. 86-96.
LOCAL j AS LONG, tmp, y, ser AS EXT
DIM cof(0 TO 13) AS LOCAL EXT
cof(0) = 57.1562356658629235
cof(1) = -59.5979603554754912
cof(2) = 14.1360979747417471
cof(3) = -0.491913816097620199
cof(4) = 0.339946499848118887e-4
cof(5) = 0.465236289270485756e-4
cof(6) = -0.983744753048795646e-4
cof(7) = 0.158088703224912494e-3
cof(8) = -0.210264441724104883e-3
cof(9) = 0.217439618115212643e-3
cof(10) = -0.164318106536763890e-3
cof(11) = 0.844182239838527433e-4
cof(12) = -0.261908384015814087e-4
cof(13) = 0.368991826595316234e-5
IF x <= 0.0 THEN FUNCTION = 0.0 : EXIT FUNCTION ' Bad argument
y = x
tmp = x + 5.2421875
tmp = (x + 0.5) * LOG(tmp) - tmp
ser = 0.999999999999997092
FOR j = 0 TO 13
y = y + 1
ser = ser + cof(j)/y
NEXT j
FUNCTION = tmp + LOG(2.5066282746310005 * ser / x)
END FUNCTION
[/code]
